Dimensions of Spacetime

 The Dimensions of Spacetime

Most of us understand dimensions from our high school experience in mathematics class of the cartesian coordinate system. We started with the line of different lengths, then the two-dimensional objects of Euclid geometry and touched on three-dimensional space with objects like spheres, cubes, and pyramids. Some students thought a little further when understanding the motion of three-dimensional objects with respect to time and often we would use one variable mapped to time to explore its behaviour on a two-dimensional chart. The interesting thing about time though is that we never can seem to go backwards in time, and it is always the independent variable that only increases, but most equations can be run backwards, and they still work out without you having to step through a time tunnel or jump into a police box.

Spacetime – What is it?

When the Greek geometers drew out their squares, triangles and circles they drew them in sand or on papyrus, that was the space that two-dimensional geometry lived on. It was an abstraction, but that abstraction could easily be projected into the world for more practical purposes such as land division, carpentry, and masonry. Even though those trades were dealing with three dimensions of our world their surfaces were in face two dimensional. What did they think of the space around them, did they question what it was made of?

Well, they did think of it as if it was like a stage, it seems, but paid more attention to the objects in space than they did to space itself. The ancient Greeks thought about the stars differently than we do now. They believed the stars to be unchanging and perfect. Aristotle believed that the Earth was the center of the solar system, the center of everything though I don’t find anything that speaks to space itself.

The ancient Greeks divided time into an abstract chronos-time, like the timing of a clock, and a kairos-time, conditions when an action or event occurs. Their spatial counterparts, topos, their geometry and chora, a sort of abstract space so I understand. They did seem to have the notion of space and time with a relationship between the two as useful as complements to the omnipresent and abstract understanding of time and space as clock-time and geometry.

Newton considered space, the manifold, like a stage where everything took place and time as a clock that was wound up once at creation and continued to unwind setting the pace of the events that took place in space. The equations that Newton set out all had space and time somewhere in them as an integral part of the place their results existed, but it never really addressed space or time directly as an entity itself.

Einstein did begin to think about this strange phenomenon we call space and its associated partner in crime called time so much so that he wrote a treatise of it called relativity.

Quantum mechanics seemed to take the manifold of space and time for granted and basically treated it as an arena where events could or could not happen at the same time and through Everett added another dimension to the universe.

Many of us have also explored the dimension of probability. You may not think of it as a dimension but applied to the probable paths of wavicles (my word for wave/particles) and Schrodinger’s equation it appears that there are other places other timelines running alongside what you and I perceive. This was first demonstrated in the dual slit experiment and in nuclear decay when nuclei give up their neutrons. In these situations, things become truly random, probabilistic.

With Everette’s many worlds interpretation of the probabilistic behaviour of the quantum then we can add an additional axis, another dimension to space-time. This axis of course, carries all the other dimensions with it.

Anytime there is another probable path then it is taken.

The Five dimensions of Spacetime

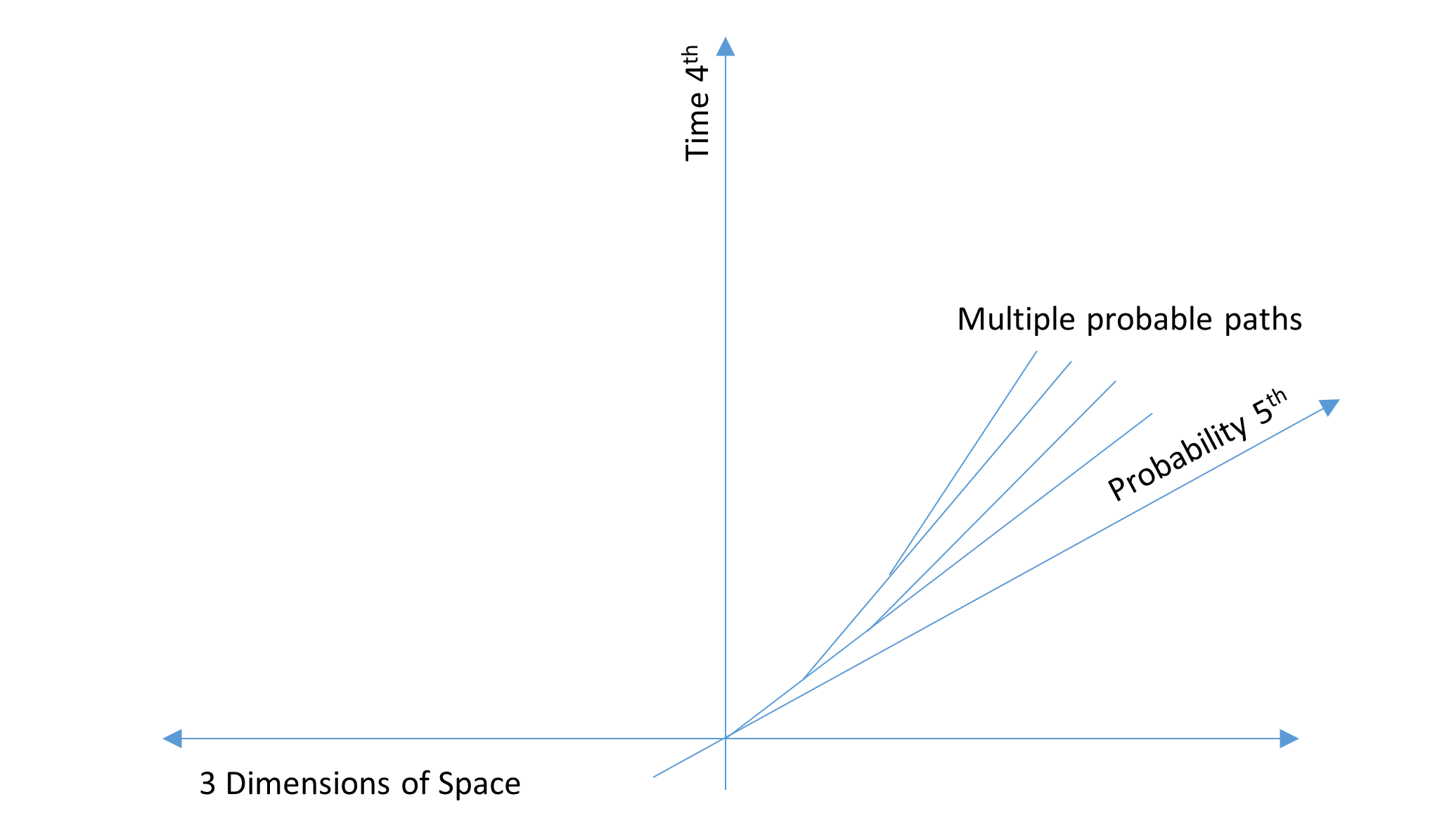
The many-worlds interpretation is a physicist name DeWitt's popularisation of what Everett hypothesized, who had referred to the combined observer–object system as split by an observation, each split corresponding to the different or multiple possible outcomes of an observation. These splits generate a tree, as shown in the attached graphic.

Everett proposed that instead of modeling an isolated quantum system with an external observer, one could mathematically model the object and include the observer and the equipment. This gets rid of the need of wave function collapse to explain the behaviour of the dual slit experiment. The photon along with the equipment and its observers exist in multiple states, many worlds. .